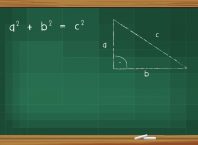
Il Teorema di Euclide riporta quanto segue: in termini matematici, se chiamiamo i lati del triangolo rettangolo A, B e C, con C come ipotenusa, allora il teorema può essere sintetizzato con la seguente formula:
C^2 = A^2 + B^2
Il Teorema di Euclide è di fondamentale importanza nella geometria e ha diverse applicazioni pratiche.
È comunemente utilizzato nella risoluzione di problemi relativi alle misure dei lati di un triangolo rettangolo e alla determinazione delle relazioni tra le sue dimensioni.
Qual è il primo Teorema di Euclide?
Il primo Teorema di Euclide, conosciuto anche come Teorema di Euclide sul massimo comune divisore (MCD), afferma che: “Se un numero divide entrambi i numeri A e B, allora divide anche la loro somma e la loro differenza”.
In sintesi, se abbiamo due numeri interi A e B e un terzo numero intero Z che divide sia A che B (cioè A è divisibile per Z e B è divisibile per Z), allora Z divide anche la somma di a e b e la loro differenza.
La formula che esprime matematicamente il primo Teorema di Euclide è la seguente:
Se Z divide A e B, allora x divide anche (A + B) e (A – B)
Questo teorema ha varie applicazioni, specialmente nella teoria dei numeri e nell’algebra, dove viene utilizzato per provare proprietà e relazioni tra i numeri interi.
Come si risolve il Teorema di Euclide?
Il teorema di Euclide non è un problema da risolvere, ma una proposizione matematica che afferma una relazione tra i lati di un triangolo rettangolo.
Per cui non esiste un processo di risoluzione specifico per il teorema di Euclide.
Tuttavia, il teorema di Euclide può essere utilizzato come strumento per risolvere problemi specifici che coinvolgono i lati di un triangolo rettangolo.
Di seguito sono riportati i passaggi generali per risolvere un problema utilizzando il teorema di Euclide:
- Leggi il problema e identifica le informazioni fornite sui lati del triangolo rettangolo;
- Assegna nomi ai lati del triangolo rettangolo, come ipotenusa (solitamente indicata con C) e i cateti (di solito indicati con A e B);
- Utilizza il teorema di Euclide, c^2 = a^2 + b^2, per stabilire l’equazione che lega i lati del triangolo rettangolo;
- Risolvi l’equazione per trovare il valore di un lato mancante, se necessario;
- Utilizza ulteriori informazioni dal problema, come l’area o la lunghezza di altri segmenti, per risolvere il problema specifico;
- Controlla la soluzione ottenuta e verifica che sia coerente con le condizioni e le restrizioni del problema.
È importante notare che il teorema di Euclide è solo uno strumento matematico per risolvere problemi relativi a triangoli rettangoli.
L’applicazione pratica del teorema richiederà l’uso di altre formule e metodi matematici in combinazione con il teorema stesso.
Il secondo Teorema di Euclide
Il secondo Teorema di Euclide è noto anche come teorema delle aree nel contesto dei triangoli rettangoli.
Il secondo Teorema di Euclide afferma che: “In un triangolo rettangolo, l’area del quadrato costruito sull’altezza relativa all’ipotenusa è uguale all’area del rettangolo che ha come dimensioni le proiezioni dei cateti sull’ipotenusa”.
Da un punto di vista matematico, se chiamiamo il triangolo rettangolo ABC, con l’ipotenusa AB e gli angoli retti in C e se H è l’altezza del triangolo tracciata dall’angolo C verso l’ipotenusa AB, allora avremo (secondo il Teorema) la seguente formula:
Area del quadrato costruito su AB = Area del rettangolo con dimensioni AC e CB
Se poi indichiamo con S l’area del quadrato e con R l’area del rettangolo, il teorema può essere espresso come:
S = R
Questo teorema è un importante risultato nella geometria dei triangoli rettangoli e può essere utile per calcolare aree e relazioni tra le dimensioni dei triangoli rettangoli.
Redazione